「サイコロを6回ふって、少なくとも1回「1の目」がでる確率について。
太郎くんは“振る各回に「1」の出る確率は1/6。だから6回振ったら
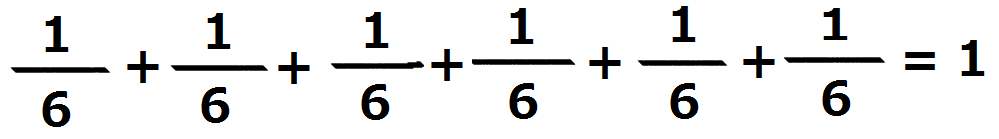
だから必ず「1」の目が出る”
こう言いました。太郎くんの言ったこれの当否を数学的に説明してください」
<別解>スタート(基本的な説明もふくみます)
ではこの「問題」においては(さいころを6回振って~)
知りたい確率とは

これです。(この分数の値です)
分子「少なくとも1回「1」の目がでるケースの合計」=A
分母「6回さいころを振ったときの出目の全組み合わせ」=B
と以下では書きます。
Aは
「6回振ったときの全部の出目の組みあわせ数」-「 「1」の目が6回中1回も出ない出目の組み合わせの数」
です。
こう考えれば、「6回中、どっかしらに「1」の目が出ている」ことになります。
(*これ以外の方針でいくと、「1」の目の出る「回数」で場合分けが生じて、「回数」ごとに数えることになります。たいへんになります。)
そして、引き算される右側とは、それを言い直すと「6回中、6回とも「1」以外の5種類の出目しかでない」、その総数となります。
これを数字に直すと
66-56(=6x6x6x6x6x6-5x5x5x5x5x5)
Bは、
6種類どれでもいいものを6列組みあわせる、これと同じですから
(*もし「2回振る」だったら、左側に1~6の6つ、右側に1~6の6つ。左右から1つずつとってどう組み合わせてもいい。
その組み合わせの合計数が「2回」振るときのサイコロの出目の全通り。 それは6×6。では、それが「6回振る」だったら?)
66(=6x6x6x6x6x6)
したがって、問題になっている確率とは
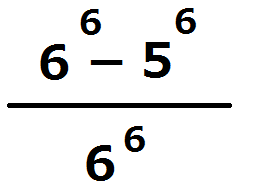
これは1ではない。〔別解終了〕
問題集などでは、この問題の「模範解答」を「排反でないものを、排反として出しているから正しくない」。こんな感じで終わりにしています。(分かります?)
分子に「-56」がなければ値は1ですが、以上のようにきちんと出すと分子は「66-56」。
分子は「66-56」と引き算されているので、
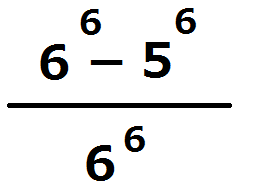
この値は1ではありません。1より小さいです。
太郎くんは感覚的に確率が1、100%と言っていますが、これまでのようにきちんと考えて出たその分数を小数に直すと約「0.665」です。
かたや(太郎くんは)感覚で100%と言っていますが、きちんと出すと正しくは約「66.5%」です。
33%以上の違い。食い違いがずいぶん大きいですね。
問題になっている確率とは
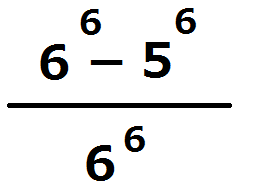
よくある問題集の「模範解答」、「排反でないものを、排反として出しているから正しくない」(それでわかります?)
*当ブログの筆者の略歴;一橋大学・卒。プロ家庭教師。講師歴;サピックス、駿台予備校、医学部専門予備校、など。合格実績;東大、京大、大阪大学(医・医)、名古屋大学(医・医)、東北大学(医・医)、九州大学(医・医)、など。